手写实现矩阵乘 Matmul
目前,在训练和推理大型深度学习模型期间,矩阵乘法可能是最重要的算法之一。本文我们将手写实现矩阵乘法,以便更好地理解矩阵乘法的原理。
CUDA 层次结构
在CUDA编程模型中,计算按照三级层次进行排序。每次调用CUDA内核都会创建一个新的网格,该网格由多个块组成。每个块由最多1024个单独的线程组成。这些常数可以在CUDA编程指南中查找。处于同一块内的线程可以访问相同的共享内存区域(SMEM)。
块中的线程数可以使用一个通常称为 blockDim 的变量进行配置,它是一个由三个整数组成的向量。该向量的条目指定了 blockDim.x、blockDim.y 和 blockDim.z 的大小,如下图所示:
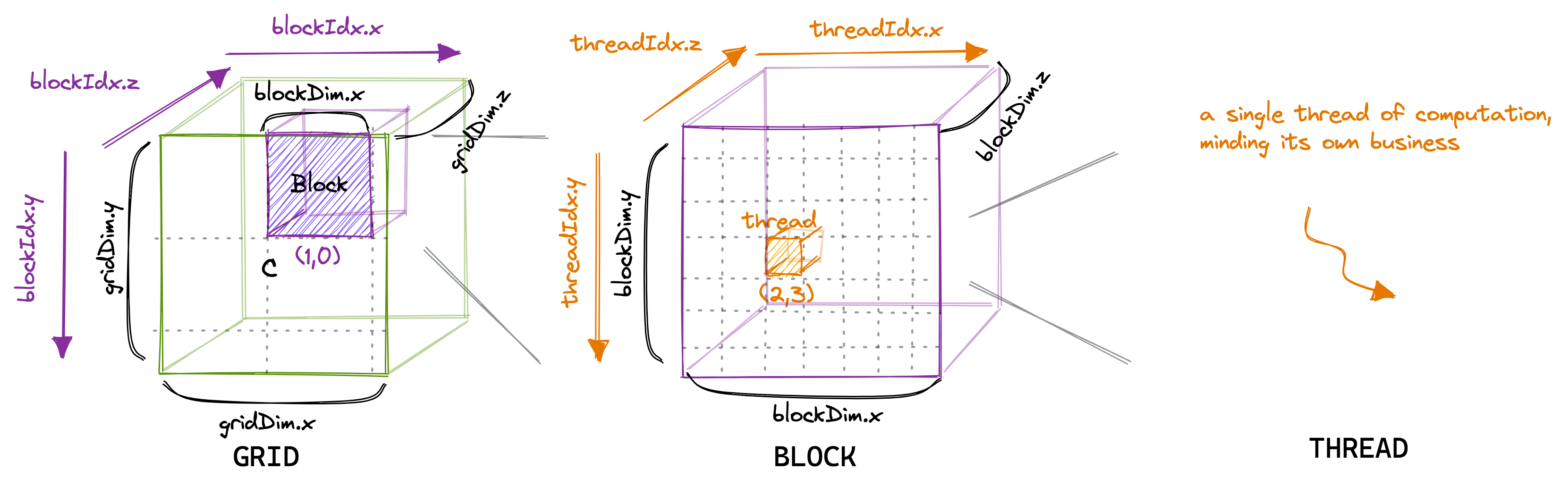
同样,网格中的块数可以使用 gridDim 变量进行配置。当我们从主机启动一个新的内核时,它会创建一个包含按照指定方式排列的块和线程的单一网格。
对于我们的第一个内核,我们将使用 grid、block 和 threa 的层次结构,每个线程计算结果矩阵C中的一个元素。该线程将计算矩阵A相应行和矩阵B相应列的点积,并将结果写入矩阵C。由于矩阵C的每个位置仅由一个线程写入,我们无需进行同步。我们将以以下方式启动内核:
#define CEIL_DIV(M, N) (((M) + (N)-1) / (N))
dim3 gridDim(CEIL_DIV(M, 32), CEIL_DIV(N, 32), 1);
// 32 * 32 = 1024 thread per block
dim3 blockDim(32, 32, 1);
sgemm_naive<<<gridDim, blockDim>>>(M, N, K, alpha, A, B, beta, C);
内核实现
CUDA代码是从单线程的视角编写的。在内核代码中,我们使用 blockIdx 和 threadIdx。这些变量的值会根据访问它们的线程而异。在我们的例子中,threadIdx.x 和 threadIdx.y 将根据线程在网格中的位置从0到31变化。同样,blockIdx.x 和 blockIdx.y 也将根据线程块在网格中的位置从0到 CEIL_DIV(N, 32) 或 CEIL_DIV(M, 32) 变化。
__global__ void sgemm_naive_kernel(float *A, float *B, float *C, int M, int N, int K)
{
const uint x = blockIdx.x * blockDim.x + threadIdx.x;
const uint y = blockIdx.y * blockDim.y + threadIdx.y;
if (x < M && y < N)
{
float sum = 0.0f;
for (int i = 0; i < K; i++)
{
sum += A[x * K + i] * B[i * N + y];
}
C[x * N + y] = sum;
}
}
下图可视化了我们的内核的执行方式:
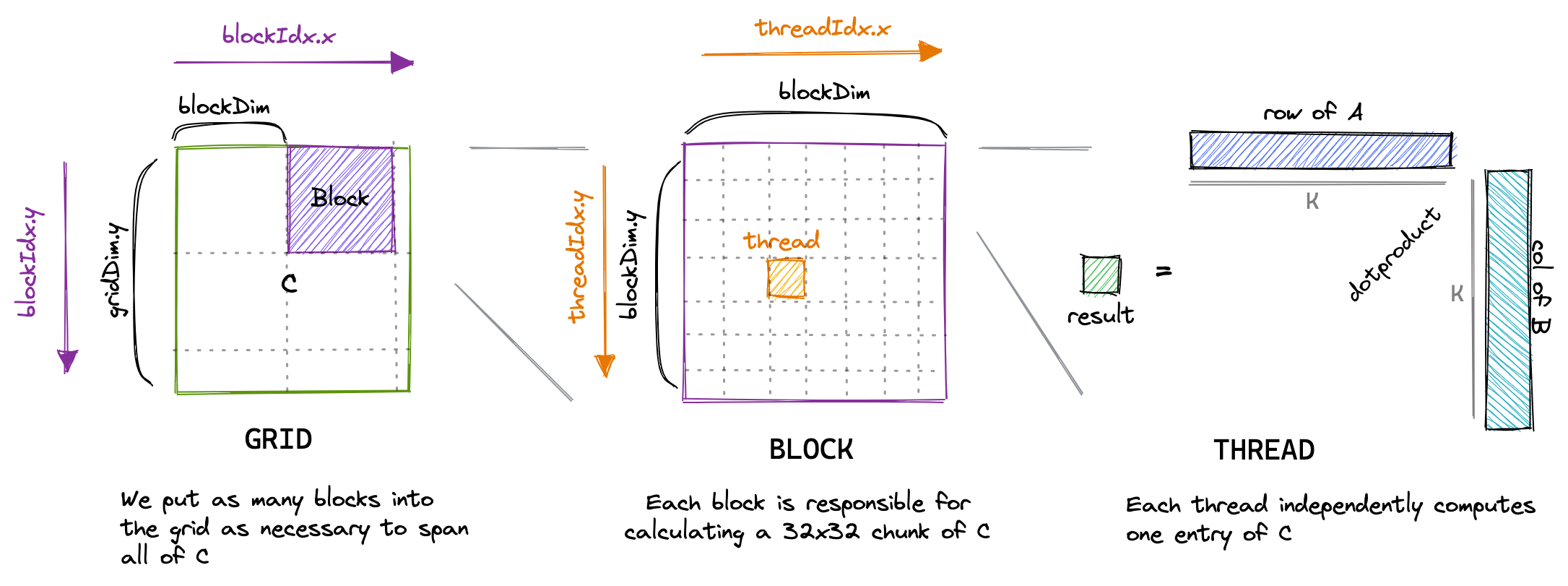
运行命令:
nvcc -o matmul_raw matmul_raw.cu
./matmul_raw
本文中我们使用的是最简单的矩阵乘法算法,下一篇文章我们将介绍更高效的矩阵乘法算法。